Теория отрисовки графов

Это продолжение рассказа об отрисовке графов. Начало можно найти тут: Нарисовать граф красиво.

Когда берешься за отрисовку графа даже сложно с ходу сообразить, а с чего начать-то? Что неудивительно, потому что задача отрисовки графов не такая уж и простая. Сначала надо определиться что понимается под словами "нарисовать красиво". Всякие разные исследования по этому поводу приходят к следующим, не таким уж и неожиданным выводам: Если вершины друг на друга заползают, если ребра пересекаются, то человеку с этим сложнее разобраться, нежели когда не заползают и не пересекаются. Некоторое влияние на восприятие графа оказывает и количество изгибов ребер, но уже в меньшей степени. Кроме красивой отрисовки нужно еще, чтобы результирующий граф уместился на какой-то площади, обычно это лист бумаги, A4, ну или больше...

Книга по отрисовке графов, которую везде рекомендуют - это Graph Drawing Algorithms for the Visualization of Graphs.

Ее авторы, Иоаннис Толлис (Ioannis G. Tollis), Джузеппе ди Батиста (Giuseppe Di Battista), Питер Эйдс (Peter Eades) и Роберто Тамассия (Roberto Tamassia)- известные специалисты в области теории отрисовки графов. На их сайтах есть ссылки на различные материалы и на их работы по отрисовке графов. На сайте Тамассии есть введение в теорию отрисовки графов (.pdf). Толлис и Тамассия являются главными редакторами журнала Journal of Graph Algorithms and Applications, на сайте которого есть статьи в электронном виде, в том числе и статьи по отрисовке графов.

Методы и подходы при отрисовке графов применяются самые разные, выбор метода зависит от того, какой именно граф требуется отрисовать. Я не буду приводить пошаговое описание алгоритмов, просто опишу какие они бывают, а пошаговые описания есть по ссылкам.
Многие алгоритмы накладывают различные ограничения при отрисовке графа в 2Д. Например: граф должен быть планарным. При ортогональной отрисовке графа часто накладывается ограничение и на степень графа - не больше четырех.

Картинка из статьи Comparing and Evaluating Layout Algorithms within GraphEd

Но можно растянуть узлы по вертикали и/или горизонтали, тогда ограничение на степень графа при ортогональной отрисовке отпадет. Но и сам алгоритм при этом усложняется.

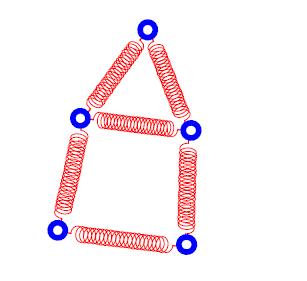
Интересный метод, которых годится для любых графов. Ребра представляются в виде пружин, нужно уменьшить эенергию системы. (Картинки из Tutorial on Graph Drawing)

Мне особенно нравится метод Сугиямы. В его основе лежит довольно простая идея: расположить вершины графа по иерархии, а потом переставить их таким образом, чтобы по максимуму убрать пересечения.

Картинка из статьи On automated graph layout

Но он годится только для направленных графов и не расчитан на отрисовку графов, содержащих циклы.

Отрисовать граф в трехмерном пространстве несколько сложнее. И методы тут применяются соответствующие.
Например вот такой: отрисовать граф в гиперболическом пространстве. Гиперболическая геометрия берет постулаты Евклида, убирает пятый, и предполагает, что через точку можно провести более одной прямой, паралелльной данной. В работе Graph visualization and navigation in information visualisation об этих методах говорится буквально следующее. "Гиперболические отображения окружены чем-то вроде тайны, потому что очень немногие люди, занимающиеся визуализацией информации, действительно понимают математику гиперболической визуализации.". Нехалявный метод, короче. Когда речь идет об этом методе тут же дают ссылку на работу Тамары Мунцнер (Tamara Munzner). На сайте есть описание и готовая реализация с исходниками H3Viewer.


Эта работа лежит и в основе упомянутого мною ранее Walrus'а.

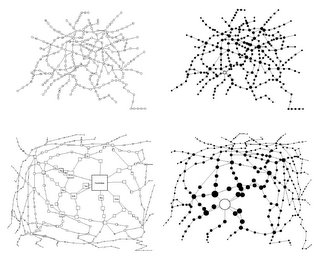
Одной из проблем отрисовки графов является то, что при определенных обстоятельствах часть вершин видна на будет. В 2Д эта проблема возникает, когда узлов слишком много, в 3Д часть узлов будет загорожена другими узлами при определенных углах зрения. Для отрисовок в таких ситуациях используются всякие разные подходы. Один из наиболее простых и понятных: объединение вершин в группы, кластеры. Очень хорошо решает проблему с большим количеством узлов.

Метод "Рыбий глаз" (Fisheye distortion) деформирует отображение графа таким образом, чтобы вершины, находящиеся в фокусе внимания были лучше видны.

Картинка из статьи Graphical Fisheye Views of Graphs

Для трехмерных случаев проблема с загораживанием хорошо решается с помощью прозрачности. Интересное применение прозрачности в работе The Information Cube.



Много работ посвящено отрисовке графов файловых систем, так как эта задача возникает довольно часто.
Файловая система силиконовских станций была показана в фильме "Парк Юркского периода" с помощью 3D File System Navigator. Это одна из первых отрисовок графа в 3Д получившая широкое распространение.



Очень красиво выглядит файловая система, отрисованная в виде дерева. Ветки и листья на деревьях расположены таким образом, чтобы они были освещены как можно больше. То есть, если смотреть со стороны солнца, их лучше всего видно. В работе Botanical Visualization of Huge Hierarchies листьев нет, листья они заменили фруктами. Ну это они называли это фруктами, на самом деле это такие, довольно абстрактные фрукты.

Учитывая прогресс в современной генетике, я думаю, что довольно скоро можно будет похачить генетический код какого-нибудь растения и вырастит структуру, аналогичную файловой системе у себя на столе. А потом гостям хвастаться "посмотрите, что у меня здесь в горшочке растет, ни за что не догадаетесь".


Ссылки по теме:
Graph Drawing на wikipedia.org
Links about Graph Drawing
Advances in the Theory and Practice of Graph Drawing статья Роберто Тамассия об отрисовке графов
Толковый словарь по теории графов
"Опрокинутый мир", Кристофер Прист - научно-фантастический роман о тяготах жизни в гиперболическом мире

Книги по теме:
Graph Drawing: Algorithms for the Visualization of Graphs
Drawing Graphs : Methods and Models (Lecture Notes in Computer Science)
Planar Graph Drawing (Lecture Notes Series on Computing)
Graph Drawing and Applications for Software and Knowledge Engineers